Round 91 to the nearest ten and delve into the captivating world of numbers, where precision meets simplicity. This comprehensive guide will unveil the secrets of rounding numbers, empowering you with the knowledge to tackle calculations with confidence and ease.
From understanding the concept of rounding to exploring practical applications, this journey through the realm of numbers promises to be both enlightening and enjoyable.
Rounding Numbers

Rounding numbers is a mathematical operation that simplifies a number by approximating it to a specific place value. Rounding to the nearest ten means approximating a number to the closest multiple of ten.
How to Round to the Nearest Ten
To round a number to the nearest ten, follow these steps:
- Identify the digit in the tens place.
- If the digit in the ones place is 5 or greater, round up the tens digit by one.
- If the digit in the ones place is less than 5, leave the tens digit unchanged.
Examples of Rounding to the Nearest Ten
- 25 rounded to the nearest ten is 30 (tens digit 2, ones digit 5, so round up).
- 43 rounded to the nearest ten is 40 (tens digit 4, ones digit 3, so round down).
- 67 rounded to the nearest ten is 70 (tens digit 6, ones digit 7, so round up).
Methods for Rounding
Rounding numbers to the nearest ten involves adjusting the value to the closest multiple of ten. This technique is commonly used to simplify calculations and estimations. There are several methods for rounding numbers to the nearest ten:
Rounding by Inspection
This method involves examining the digit in the tens place. If it is 5 or greater, the number is rounded up to the next ten. If it is less than 5, the number is rounded down to the previous ten.
Example:Round 27 to the nearest ten.
- The digit in the tens place is 2, which is less than 5.
- Therefore, 27 is rounded down to 20.
Rounding by Addition
This method involves adding 5 to the number and then rounding down to the nearest ten.
Example:Round 27 to the nearest ten.
- Add 5 to 27: 27 + 5 = 32.
- Round 32 down to 30, which is the nearest ten.
Rounding by Division
This method involves dividing the number by 10 and then rounding the result to the nearest whole number.
Example:Round 27 to the nearest ten.
- Divide 27 by 10: 27 ÷ 10 = 2.7.
- Round 2.7 to the nearest whole number, which is 3.
- Multiply 3 by 10 to get the rounded number: 3 × 10 = 30.
Rounding in Different Contexts

Rounding is a mathematical technique used to simplify numerical values by removing unnecessary digits. It plays a crucial role in various fields, each with its unique requirements for accuracy and precision.
Round 91 to the nearest ten is 90, a number that’s associated with right angles and perfect squares. If you’re looking for a fun way to test your knowledge of this and other numbers, check out the get the lead out crossword . It’s a challenging puzzle that will keep you entertained for hours.
And when you’re done, you’ll have a better understanding of numbers and their relationships.
Financial Calculations
In finance, rounding is essential for accurate calculations and decision-making. Financial institutions use rounding to determine interest rates, calculate loan payments, and assess risk. Rounding to the nearest cent or dollar simplifies calculations and facilitates quick decision-making.
Scientific Measurements
Scientific measurements often involve large or complex numbers. Rounding is used to simplify these numbers and make them easier to interpret and compare. For example, scientists may round experimental data to the nearest whole number or decimal place, depending on the precision required.
Everyday Life
Rounding is also widely used in everyday life. We round numbers to simplify measurements, estimate distances, and make quick calculations. For instance, we might round the temperature to the nearest degree or round the distance to the nearest mile when planning a road trip.
Applications of Rounding

Rounding is an essential skill in many fields, providing estimates, simplifying data, and aiding decision-making. It involves approximating a number to a specified level of accuracy, usually by removing or adding digits.
Estimation
Rounding is crucial for quick estimations. For example, a store may estimate its daily sales by rounding up the number of customers to the nearest ten. Similarly, a teacher might round the average test score to the nearest whole number for easier interpretation.
Data Analysis
In data analysis, rounding helps simplify large datasets. By rounding data points to a certain precision, researchers can identify trends and patterns more easily. For instance, a survey might round respondents’ ages to the nearest decade to analyze age-related demographics.
Decision-Making
Rounding plays a role in decision-making when precise values are not necessary. For example, a company might round its projected profits to the nearest million dollars to make budgeting decisions. Rounding can also help avoid over-analyzing data and allows for more efficient decision-making.
Accuracy and Precision
Rounding plays a crucial role in determining the accuracy and precision of calculations. Accuracy refers to how close a rounded value is to the original value, while precision refers to the number of significant digits used to represent a value.
Rounding can impact the reliability of results by introducing errors. For example, rounding a value to the nearest ten may result in a significant difference from the original value, especially if the original value is close to a multiple of ten.
This can lead to inaccuracies in calculations and affect the validity of conclusions drawn from the results.
Impact on Accuracy
- Rounding can introduce errors, especially when the original value is close to a multiple of the rounding factor.
- Inaccurate rounded values can lead to incorrect conclusions and unreliable results.
Impact on Precision
- Rounding reduces the number of significant digits, which can affect the precision of a value.
- Values rounded to a smaller number of significant digits may lose important information, leading to less precise results.
Alternative Rounding Techniques

In certain scenarios, standard rounding techniques may not suffice. To address this, alternative rounding methods have been developed, offering greater flexibility and precision.
These techniques include:
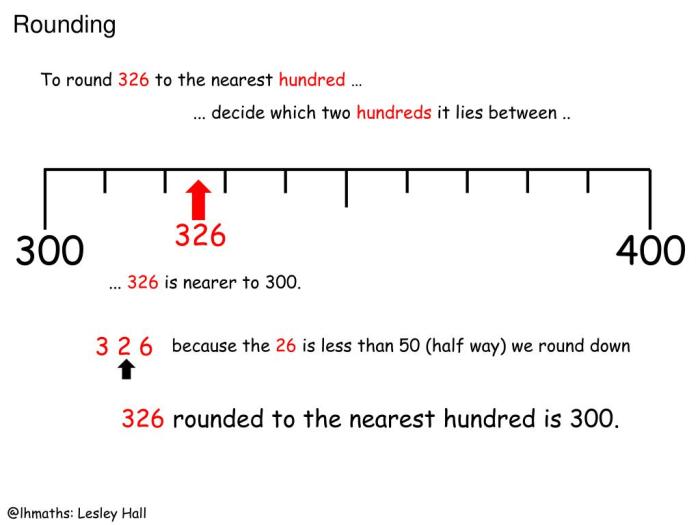
Rounding to the Nearest Hundred, Round 91 to the nearest ten
Rounding to the nearest hundred involves adjusting a number to the nearest multiple of 100. For instance, 255 would be rounded to 300, while 245 would be rounded to 200.
Rounding to a Specific Number of Significant Figures
Rounding to a specific number of significant figures entails adjusting a number to retain only the specified number of meaningful digits. For example, rounding 12.345 to two significant figures would yield 12, while rounding to three significant figures would yield 12.3.
Advanced Rounding Concepts

In addition to basic rounding techniques, there are more advanced concepts that provide greater precision and accuracy in specific scenarios.
These advanced rounding methods are designed to address situations where the standard rounding rules may not be sufficient or may introduce bias.
Midpoint Rounding
Midpoint rounding, also known as nearest even rounding, rounds a number to the nearest integer that is closest to its midpoint.
If the number is exactly halfway between two integers, it is rounded to the even integer.
Example: 4.5 is rounded to 4, while 5.5 is rounded to 6.
Banker’s Rounding
Banker’s rounding, also called commercial rounding, is a rounding method commonly used in financial applications.
In banker’s rounding, a number is rounded to the nearest integer that is closest to its value, with ties being rounded to the nearest even integer.
Example: 4.5 is rounded to 4, while 5.5 is rounded to 6.
FAQs: Round 91 To The Nearest Ten
What is the concept of rounding to the nearest ten?
Rounding to the nearest ten involves adjusting a number to the closest multiple of ten. For instance, 91 rounded to the nearest ten becomes 90.
How do I round 91 to the nearest ten?
To round 91 to the nearest ten, examine the digit in the ones place. Since it’s less than 5, we round down to the nearest multiple of ten, which is 90.
What are the practical applications of rounding?
Rounding finds widespread use in various fields, including financial calculations, scientific measurements, data analysis, and estimation.
